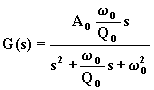
5.3. – Quadripolo passa-banda
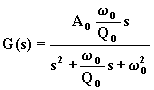
Esprimendo il denominatore in forma normalizzata e ponendo s = jw , si ottiene:
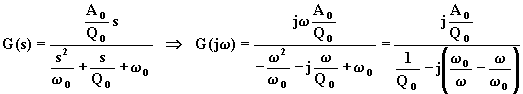 ;
;
il cui modulo e fase sono:
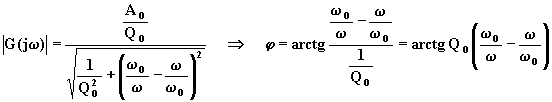
Da questi si può dedurre quanto segue:
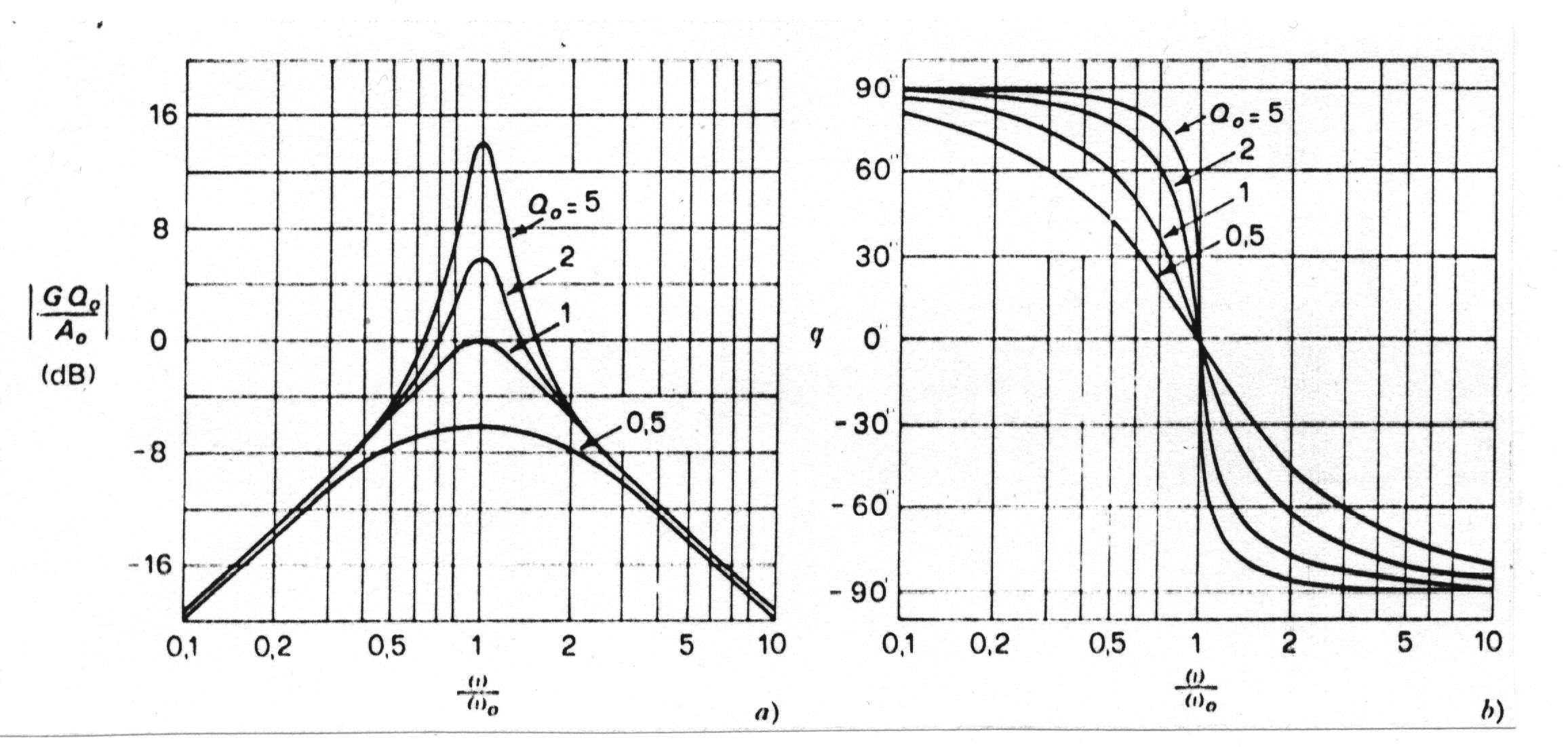
alla pulsazione di centro banda (w = w o) il modulo della f.d.t. è massimo e vale Ao; la fase è invece uguale a zero;
la curva caratteristica per il modulo presenta simmetria geometrica rispetto a w = w o; ciò significa che, indicando con w 1 e w 2 due pulsazioni (una inferiore e l'altra superiore a w o), in corrispondenza alle quali il modulo della f.d.t. è lo stesso, risulta:
![]() .
.
Affinché il modulo della f.d.t. rimanga invariato deve essere:
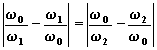 .
.
Per valori della pulsazione molto prossimi a w o, la simmetria si confonde con quella
aritmetica. In tale ipotesi, si ha:
![]() ;
;
la frequenza di taglio inferiore e quella superiore valgono rispettivamente:
![]()
Pertanto la larghezza di banda risulta:
![]() .
.
In figura sono riportati i diagrammi di Bode in funzione di w /w o con parametro Qo. Essi sono convenienti quando risulta Qo < 10 perché le frequenze di taglio si trovano nella regione a simmetria geometrica.
Quando, invece, risulta Qo > 10, le frequenze di taglio sono così prossime a fo che si trovano nella regione a simmetria aritmetica; in tale caso conviene utilizzare una scala lineare almeno per l'ascissa al fine di mettere in evidenza questa simmetria.
Qualunque sia il Qo, tutte le curve raggiungono la stessa pendenza di 40dB/decade.