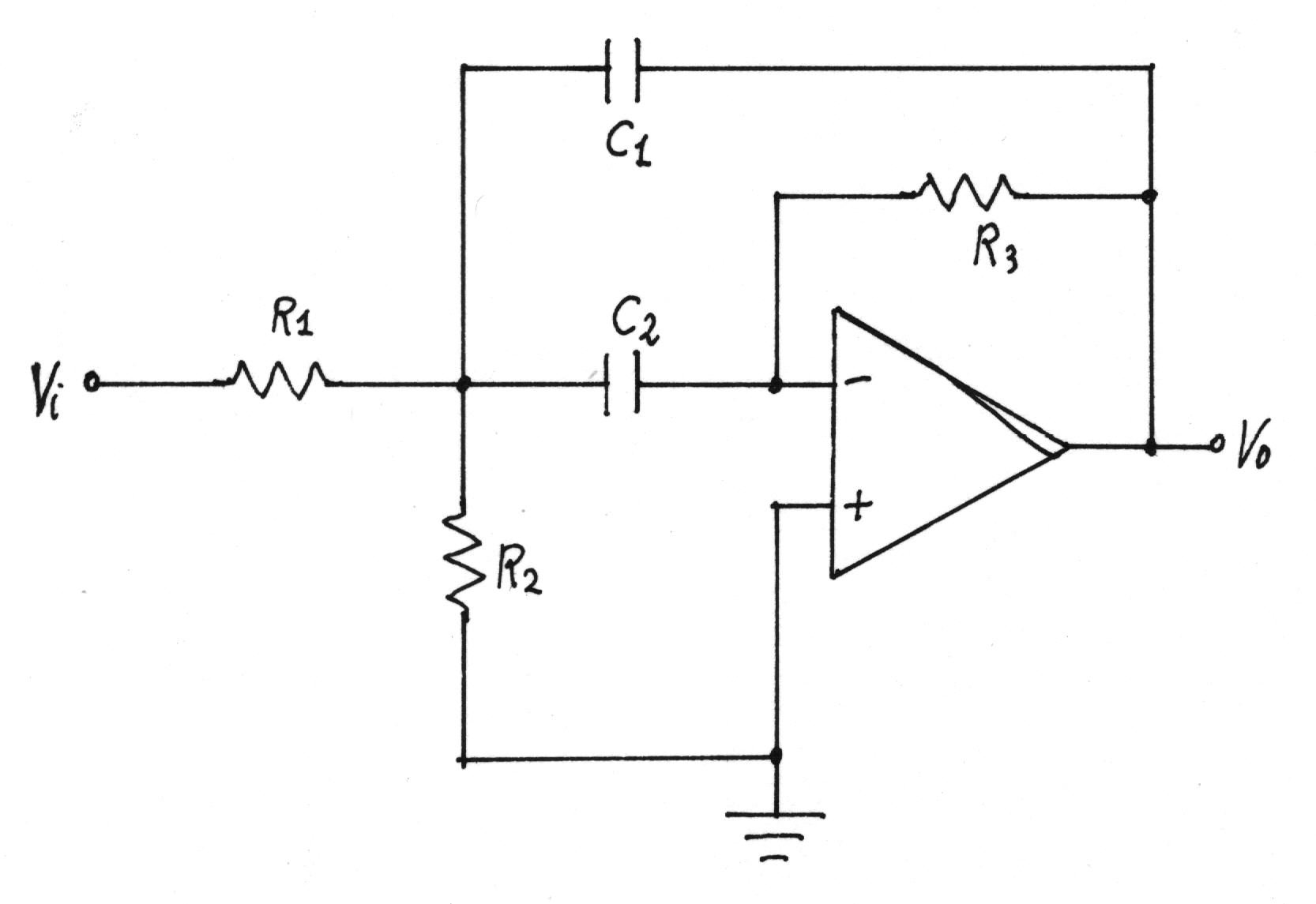
7.1.3. – Filtro passa-banda (a banda stretta)

In figura è riportato il circuito di un filtro passa-banda a retroazione multipla per Q_o < 10. Si osservi che la rete contiene due filtri RC, uno passa-alto ed uno passa-basso.

dove

Associando ad ogni Y_i la sua espressione si ha la f.d.t. del filtro:

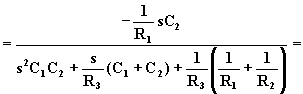
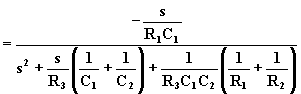
Dal confronto con la f.d.t. generalizzata

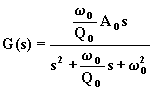
si trae:

                                                                                                                           (7.3.1)

                                                                                                                     (7.3.2)

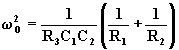                                                                                                             (7.3.3)

Sostituendo la (7.3.2) nella (7.3.1), si ottiene:

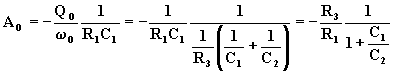                                                       (7.3.4)

Il guadagno di tensione alla pulsazione w _o non dipende dalla resistenza R₂; la pulsazione w _o, invece, dipende da tutti gli elementi.

Si può dimostrare che la sensibilità del parametro Q_o alle variazioni delle capacità C₁ e C₂ è, in tale circuito, proporzionale a Q_o. Tale circuito non è pertanto conveniente quando il Q_o diventa elevato (in pratica superiore a 10).

Per quanto riguarda i criteri di progettazione, anche in questo caso si deve verificare se è possibile scegliere arbitrariamente i valori delle capacità C₁ e C₂.

Ricavando R₃ dalla (7.3.2), R₁ dalla (7.3.1) e sostituendo nella (7.3.3), si ottiene:

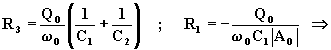
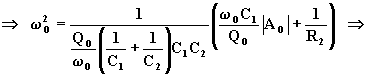
                                                                                              (7.3.5)

Affinché il secondo membro non possa diventare negativo deve essere:

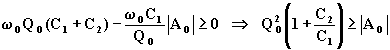                                                               (7.3.6)

Se risulta si può scegliere il valore del rapporto C ₂/C₁ in modo tale che, nella (7.3.6) sia verificata la condizione di uguaglianza:

                                                                                              (7.3.7)

In tal modo diventa minimo il numero dei componenti perché diventa R₂ = ¥ , come si vede dalla (7.3.5); è però normalmente necessario l'uso di un trimmer compensatore al fine di poter utilizzare il voluto valore per ciascuna capacità.

Il circuito diventa il seguente.

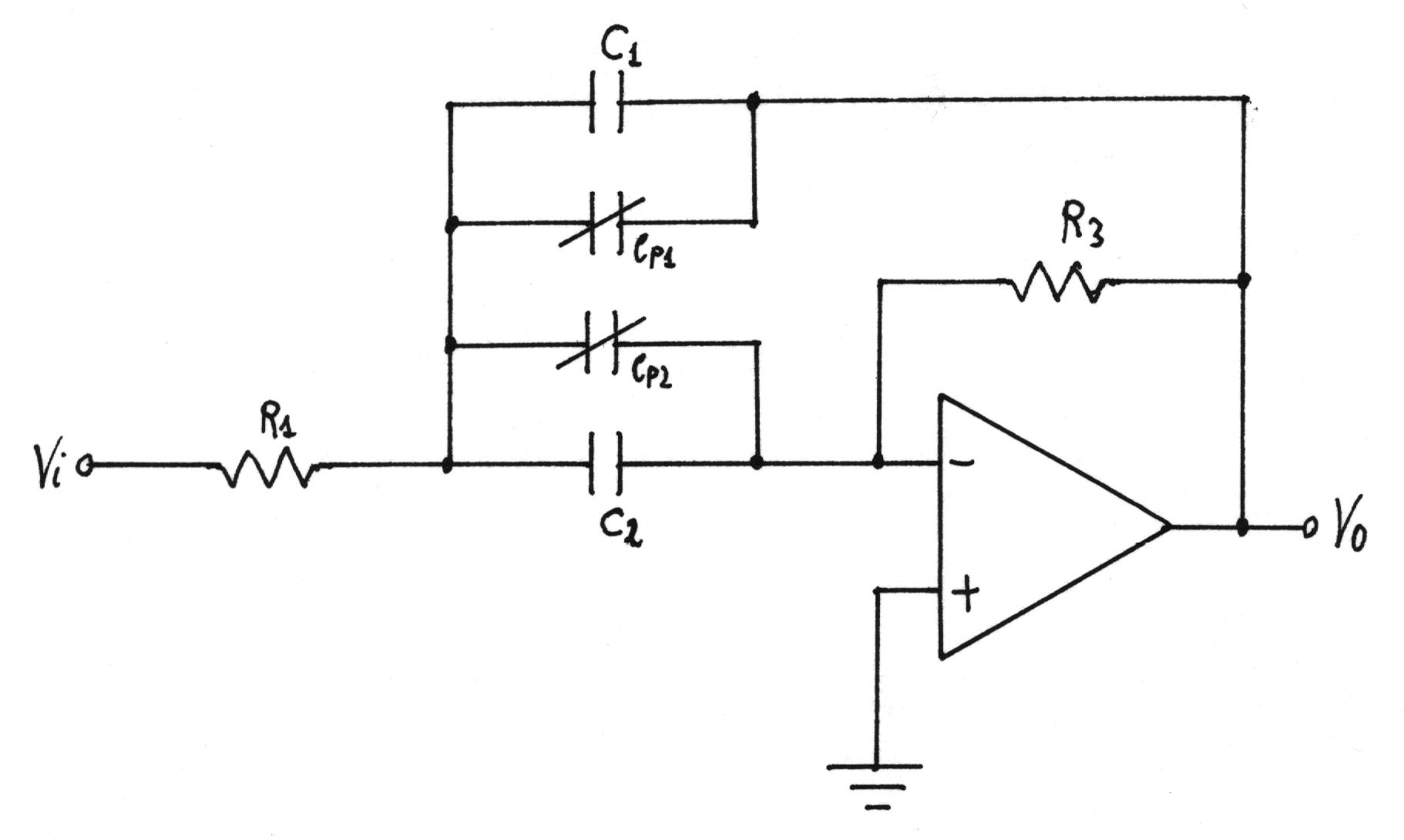
C_p1 e C_p2 sono due compensatori (trimmer capacitivi) che possono essere necessari ad ottenere gli opportuni valori di capacità.

Con si ha:

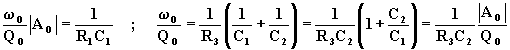
Da queste si possono ricavare R₃C₂ e R₁C₁:

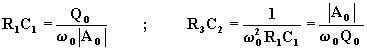
Per il progetto si procede nel seguente modo:

si determina il valore del rapporto C2/C ₁;

si determinano i valori di R₃C₂ e R₁C₁;

si assegna un valore a C₁ tale per cui risulti accettabile il valore di R₁;

si determina il valore di C₂ e dell'eventuale compensatore;

si determina il valore di R₃.

Se invece risulta si può porre C₁ = C₂ = C, semplificando in tal modo il progetto del filtro. Le equazioni (7.3.1, 7.3.2, 7.3.3, 7.3.4, 7.3.5), diventano:

                                                                                                                           (7.3.8)

                                                                                                                                   (7.3.9)

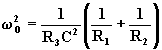                                                                                                               (7.3.10)

                                                                                                                              (7.3.11)

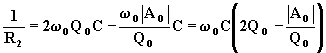                                                                      (7.3.12)

Dalla (7.3.12) si deduce R₂C

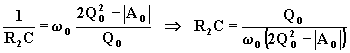
e dalla (7.3.8) la quantità R₁C:

Per il progetto si procede nel seguente modo:

si calcolano le quantità R₁C e R₂C;

si sceglie un valore di C tale che ne derivino valori accettabili per R₁ e R₂;

si ricava il valore di R₃ dalla (7.3.11).

Anche in questo caso è conveniente che il guadagno A_o non sia troppo grande.

Per valori di Q_o compresi tra 10 e 50 si deve usare il seguente circuito, con due amplificatori operazionali e una retroazione complessiva positiva.

Al fine di determinare la f.d.t. di questo circuito, indichiamo i suoi elementi con delle generiche ammettenze Y_i.

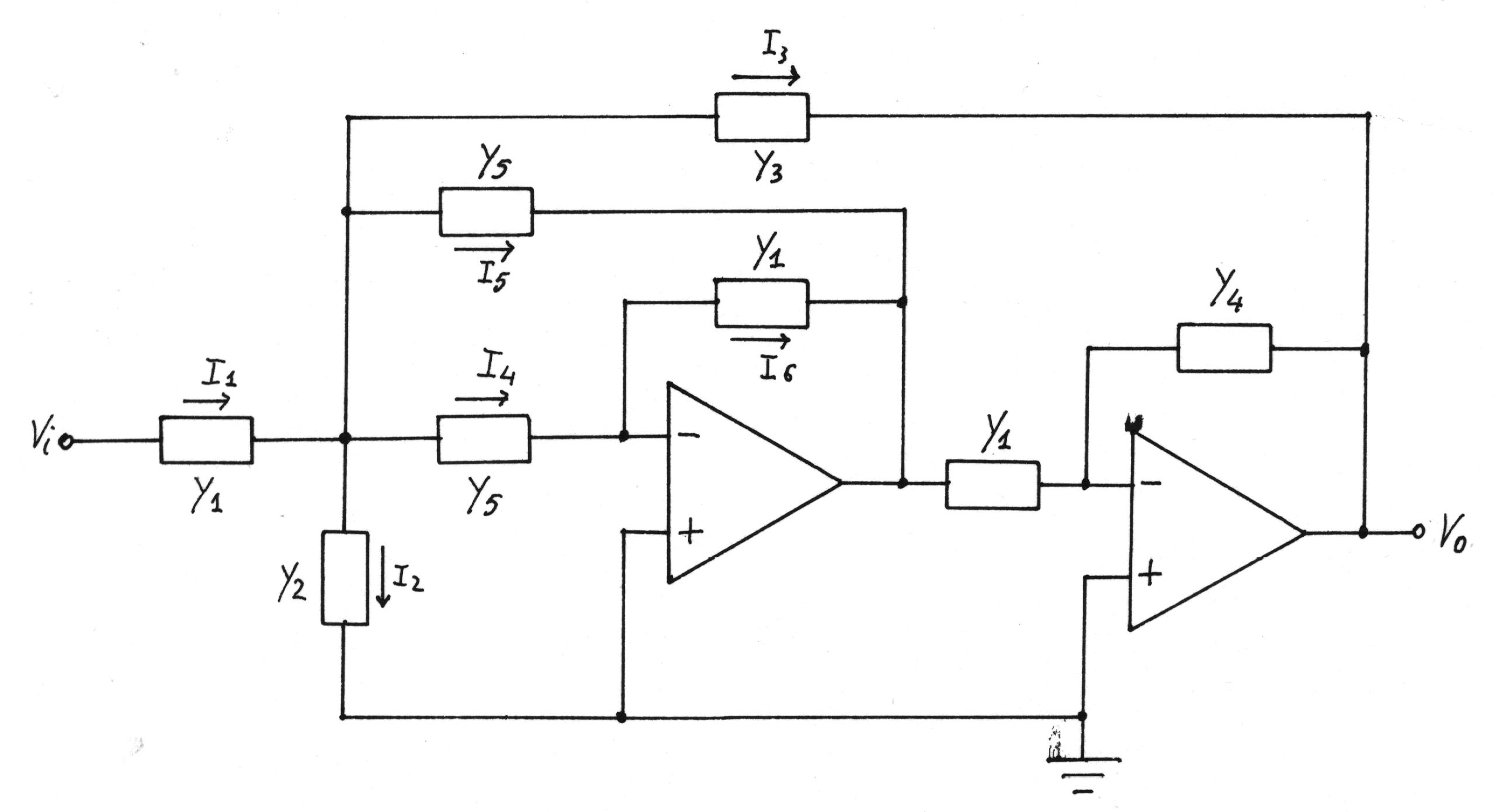
Applicando il I° principio di Kirchhoff al nodo A, si ha:

Raccogliendo i termini in V_A, si ha:

                                                                             (7.3.13)

Tenendo conto che e applicando il I° principio di Kirchhoff all'ingresso invertente del primo amplificatore operazionale, si ha:

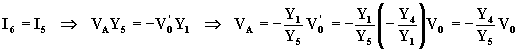
Sostituendo le espressioni così ottenute nella (7.3.13), si ottiene:

Sostituendo alle Y_i le loro espressioni si ottiene la f.d.t. del filtro.

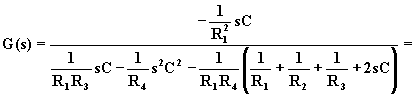
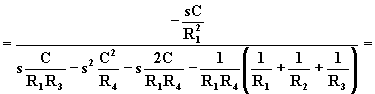
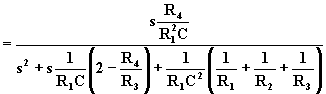
Dal confronto con la f.d.t. generalizzata

si trae:

                                                                                                                           (7.3.14)

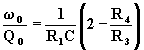                                                                                                                   (7.3.15)

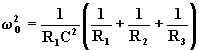                                                                                                     (7.3.16)

Perché tutti i parametri del circuito risultino positivi deve essere

Sostituendo la (7.3.15) nella (7.3.14), si ottiene:

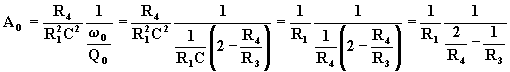
Il guadagno dello stadio di uscita, pari a R₄/R₁, è normalmente compreso tra 1 e 10 per rendere il circuito meno sensibile alle variazioni delle capacità.

Per quanto riguarda i criteri di progetto le limitazioni sono essenzialmente due:

R₄ < 2R₃, affinché tutti gli elementi risultino reali e positivi.

dalla

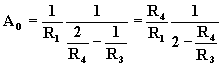
Poiché il rapporto (amplificazione del secondo operazionale)

Perché il primo membro sia positivo deve essere:

,

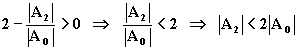cioè il guadagno del secondo amplificatore deve essere minore del doppio del guadagno complessivo.

Dalla (7.3.15) si calcola la quantità R₁C:

.

Per il progetto si procede nel seguente modo:

si fissano i valori di A_o e A₂;

si calcola la quantità R₁C;

si fissa un valore di capacità C tale per cui risulti accettabile il valore di R₁;

si calcola R₄ da

si calcola R₃ da

;

si calcola R₂ dalla (7.3.16):

.
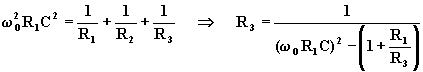