2.3.2. - Variazione della forma d'onda d'uscita al variare della frequenza

La risposta del circuito è strettamente legata al confronto tra la durata del transitorio di carica o di scarica e il semiperiodo dell'onda quadra. La durata di un transitorio, nei circuiti del primo ordine, è, in ogni caso, , dove è la costante di tempo del circuito. Pertanto, la risposta del circuito sarà determinata dal confronto di con T/2 (durata di un semiperiodo).

Se l'onda quadra d'ingresso è a valore medio nullo, tale sarà anche il segnale d'uscita; se il segnale d'ingresso è a valore medio non nullo, il segnale d'uscita avrà lo stesso valore medio (poiché la capacità si carica al valore medio del segnale d'ingresso) e oscillerà attorno ad esso.

Il transitorio si esaurisce in un tempo trascurabile rispetto alla durata della semionda. Tanto più , tanto più la forma d'onda d'uscita approssimerà l'onda quadra d'ingresso.

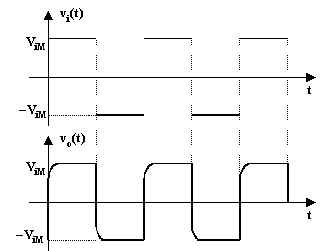
Il transitorio ha appena il tempo di esaurirsi prima che l'ingresso commuti. La forma d'onda d'uscita sarà una successione periodica di transitori completi di carica e di scarica.

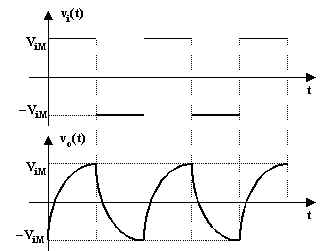
Il transitorio, in un semiperiodo, non si esaurirà, per cui l'uscita non raggiungerà più i valori e . La forma d'onda d'uscita, costituita da transitori parziali di carica e di scarica, oscillerà attorno al valore medio d'uscita tra i valori e , simmetrici rispetto al valore medio d'uscita. Nel nostro caso l'uscita oscillerà attorno allo zero, con .

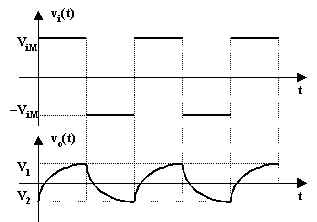
Il transitorio si evolverà solo nel primissimo tratto della curva di carica (0 di scarica), tratto iniziale che ha praticamente andamento rettilineo. Si avranno, pertanto, attorno al valore medio, rampe lineari crescenti e decrescenti varianti tra e .

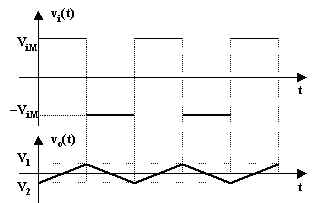
In tale caso il circuito viene detto integratore, in quanto il segnale d'uscita è proporzionale all'integrale del segnale d'ingresso. L'integrale di un segnale ad onda quadra è, infatti, un segnale ad onda triangolare.