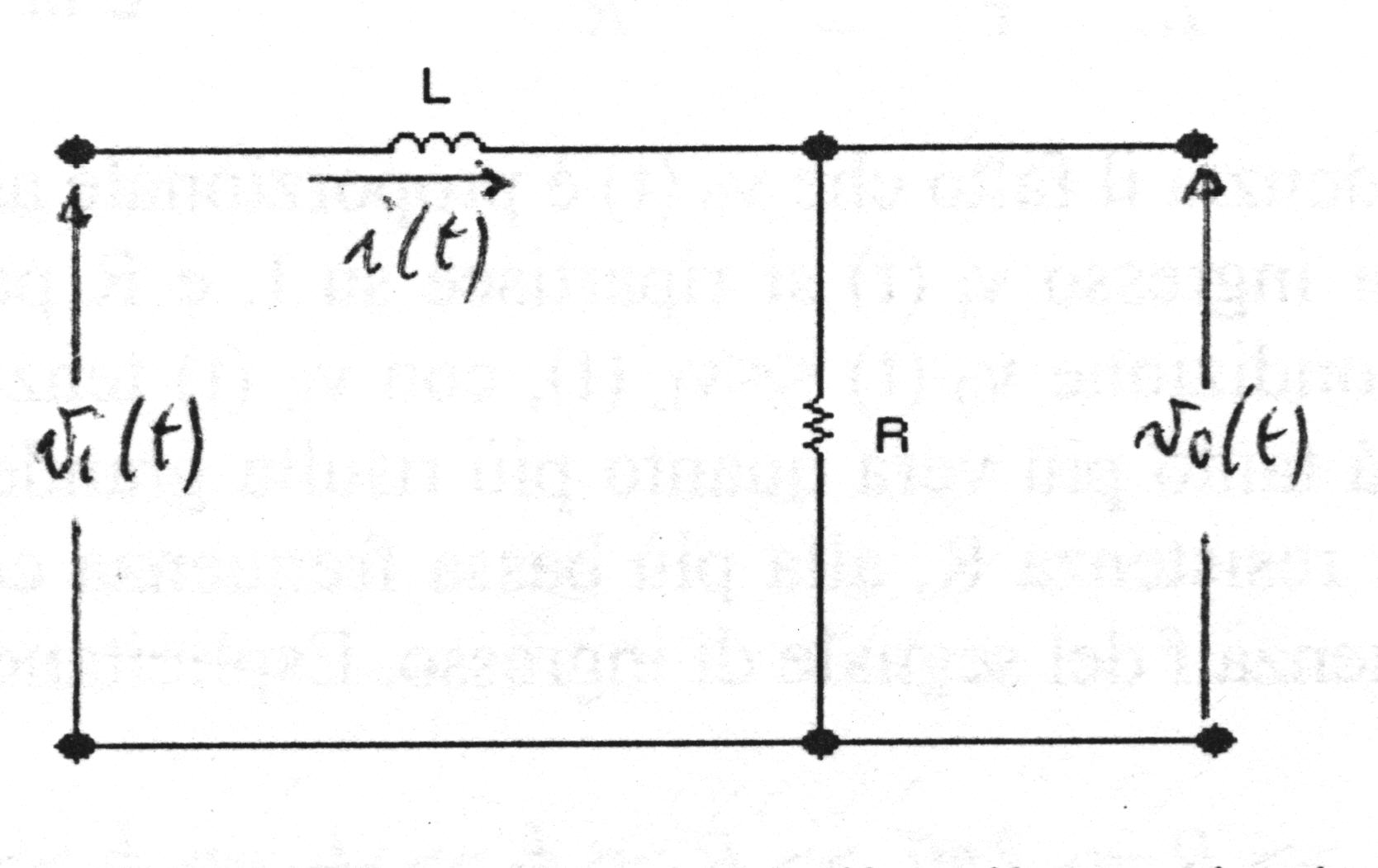
1.1.2. - Integratore con rete RL

Un altro semplice circuito integratore è quello riportato in figura 1.3, realizzato con una resistenza R e un’induttanza C.

Fig. 1.3

Al fine di ottenere l’uscita in funzione dell’ingresso, si applica il II principio di Kirchhoff al circuito di figura:

                                                                                                                            (1.5)

La relazione che lega la tensione ai capi di una induttanza con la corrente che vi circola è:

Poiché

Sostituendo nella (1.5), si ha:

Si risolve rispetto dv_o(t)

Integrando membro a membro si ha:

                                       (1.6)

Nel caso risulti v_o(t) << v_i(t), si può trascurare, nell’integrale a secondo membro, v_o(t) rispetto a v_i(t), ottenendo con buona approssimazione:

                                                                          .                                             (1.7)

Se al tempo t = 0 risulta v_o(0) = 0, si ha:

                                                                                ,                                                  (1.8)

Dove è la costante di tempo del circuito.

La (1.8) evidenzia il fatto che v_o(t) è proporzionale all’integrale del segnale di ingresso.

Il segnale di ingresso v_i(t) si ripartisce su L e R per cui la condizione v_o(t) << v_i(t) equivale alla condizione v_o(t) << v_L(t), con v_L(t) tensione ai capi dell’induttanza L. Tale condizione sarà tanto più vera quanto più risulta grande il valore della reattanza induttiva X_L rispetto alla resistenza R, alla più bassa frequenza componente del segnale di ingresso ossia alla frequenza f del segnale di ingresso. Esplicitando, si ha:

Dove è la costante di tempo del circuito, f e T sono rispettivamente la frequenza e il periodo del segnale d’ingresso.

Concludendo, perché il circuito esaminato funzioni da integratore, il rapporto L/R deve risultare molto maggiore del periodo del segnale di ingresso.