3.4. - Risposta in frequenza di un integratore reale

Si è visto al paragrafo 2.2 del capitilo 2 che la funzione di trasferimento dell’integratore nella variabile s, è data da:

                                                                                                                      (3.12)

Nel caso dell’integratore reale si ha:

.

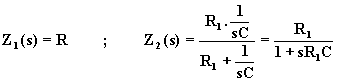Sostituendo nella (3.12), si ha:

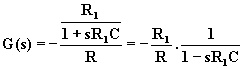                                                                                                   (3.13)

La funzione di trasferimento (3.13) non ha zeri e presenta un polo negativo p = - 1/(R₁C).

Al fine di ottenere la risposta in frequenza si suppone di lavorare in regime sinusoidale. In tale ipotesi s = jw .

Sostituendo nella (3.13), si ha:

                                                                                        (3.14)

Il cui modulo e fase sono:

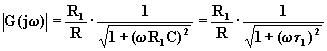                                                                                (3.15)

                                                                                       (3.16)

La risposta in frequenza si ottiene tracciando i diagrammi di Bode del modulo e della fase.

Si esprime la (3.15) in decibel:

                              (3.17)

Al fine di tracciare l’andamento asintotico, si esaminano i seguenti tre casi:

a.                                        (3.18)

che nel diagramma di Bode rappresenta una retta orizzontale che interseca l’asse delle ordinate in 20lg₁₀₍R₁/R), che corrisponde alla massima amplificazione A = R₂/R_1.

b.-                               (3.19)

che nel diagramma di Bode rappresenta una retta con pendenza negativa di 45°, ossia una pendenza di –20dB/decade, che interseca l’asse delle ascisse nel punto w = 1/t ₁, ossia w = 1/R₁C.

Le due rette ai punti a.- e b.- si intersecano nel punto dato dalla soluzione del sistema delle due equazioni (3.18) e (3.19), che determina la seguente relazione:

che è il polo dell’equazione (3.13)

Calcolando la (3.18) a w = 1/t ₁, si ha: .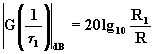

Il punto d’intersezione è quindi: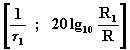

c.- 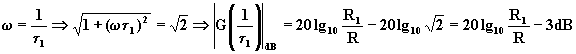                (3.20)

La (3.20) evidenzia che nell’interno del polo, la risposta effettiva si discosta dalla risposta data dal diagramma di Bode per un massimo di –3dB in corrispondenza del polo. L'ap= prossimazione ottenuta con le (3.18) e (3.19) è ben verificata per w < 0 , 1 / t ₁ e per w > 1 0 / t ₁, come evidenziato dalla fig.(3.3).

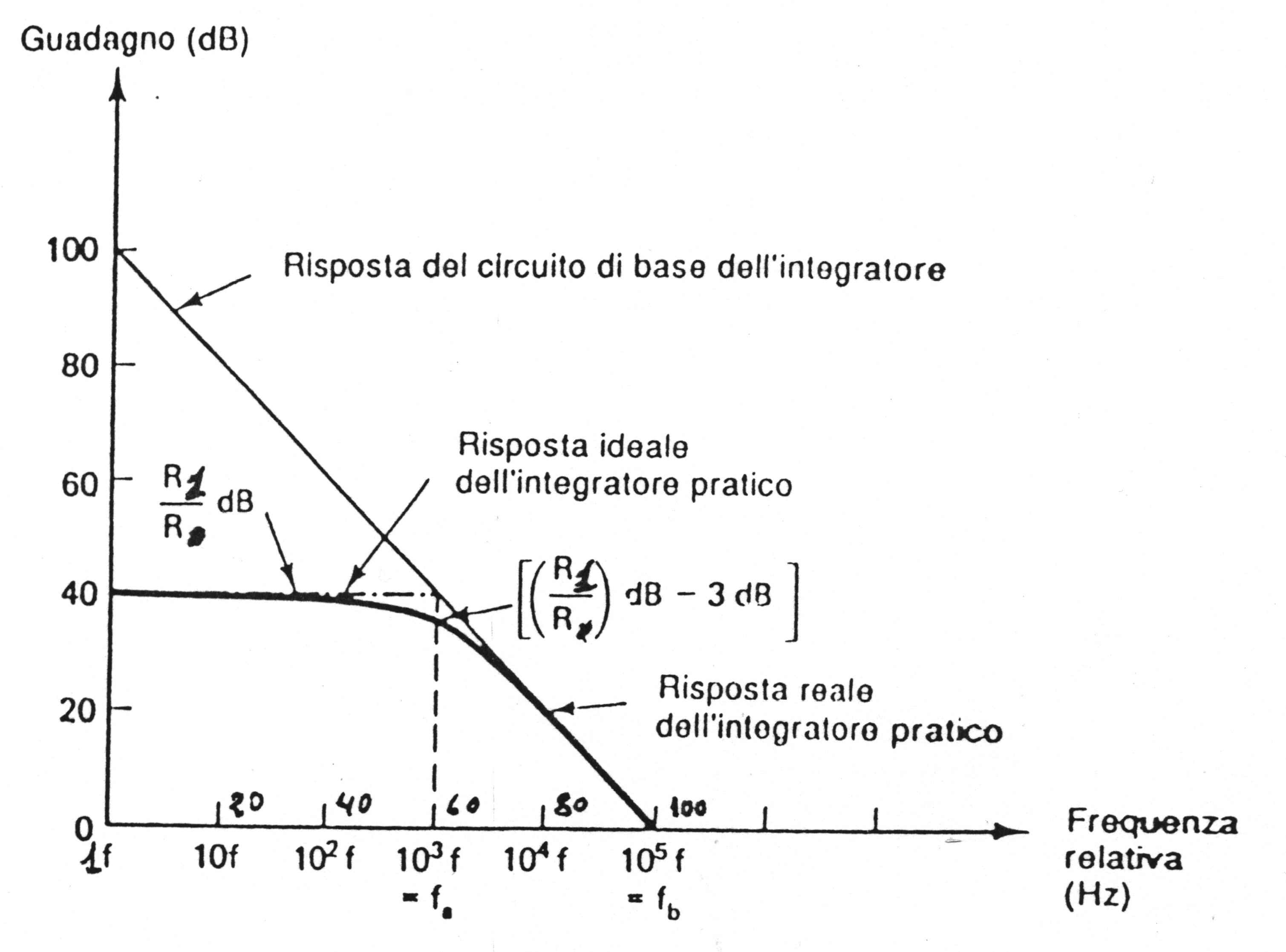
Fig. 3.3 Diagramma di Bode dall'ampiezza

La risposta in fase della funzione di trasferimento (3.4) è data dalla differenza tra la fase del numeratore (-R₁/R + j0) e la fase del denominatore (1 + jw t ₁), ossia:

j ( w ) = p - arctg( w t ₁₎ (3.21)

L’espressione (3.21) può essere rappresentata in un diagramma avente per ascissa lg_10w e per ordinata la fase, il cui andamento si ricava considerando con buona approssimazione, che:

a_.- w < 0 , 1 / t ₁ Þ arctg(w t ₁₎ @ 0 Þ j = p

b_.- w > 1 0 / t ₁ Þ arctg( w t ₁₎ @ p / 2 Þ j = p / 2

c_.- 0,1/t _{1 £} w £ 10/t ₁ Þ j è rappresentata da una retta che congiunge i punti

( 0 , 1/ t ₁ ; p ) e (1 0 / t ₁ ; p / 2 )

Per w = 1 / t ₁ si ha: j ( 1 / t ₁) = p - arctg 1 = p - p / 4 = 3 p / 4

In fig. 3.4 è riportato l’andamento di j in funzione di lg₁₀ w .

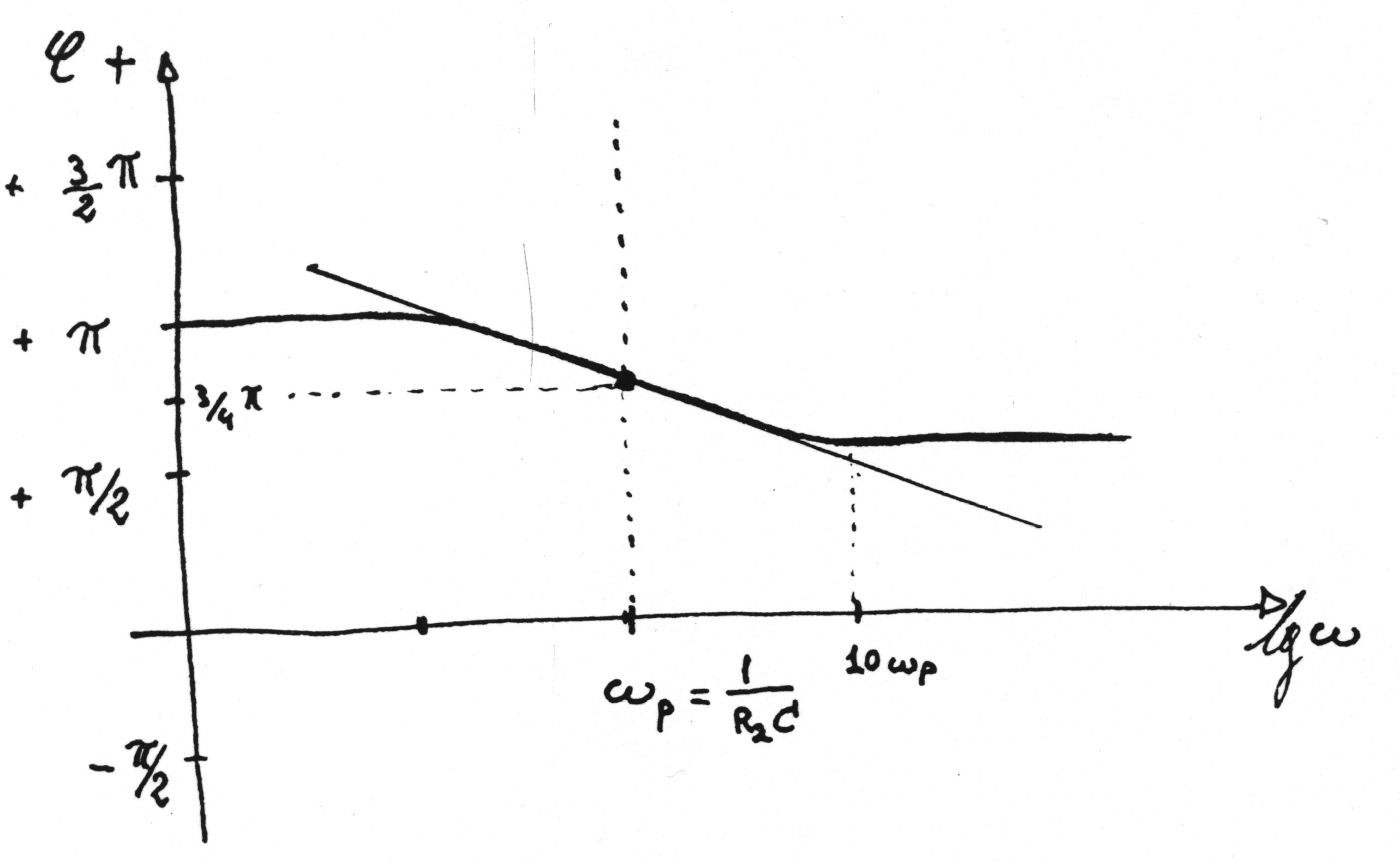
Fig. 3.4 Diagramma di Bode dalla fase

Dai diagrammi di Bode si nota che il modulo assume l’andamento di quello di un integratore per w > 1 / t ₁, mentre la curva della fase raggiunge lo sfasamento di 90^o ( in anticipo, per l’inversione dovuta alla configurazione invertente dell’operazionale ) con buona approssimazione solo per w ³ 1 0 / t ₁.

In conclusione, se f è la frequenza del segnale di ingresso, il circuito si comporta da integratore se w ³ 1 0 / t ₁, ossia f ³ 1 0 / 2 p t ₁.

La frequenza f₁ = 1 0 / 2 p t ₁ definisce un limite inferiore di frequenza.

L’estremo superiore di frequenza è fissato dal valore di frequenza per il quale il modulo del guadagno in decibel è di 0dB.

Imponendo la (3.19) uguale a zero, si ottiene:

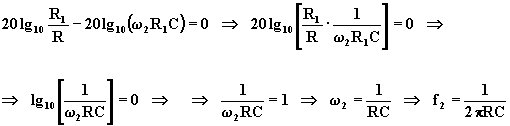
Tale frequenza rappresenta un limite superiore di frequenza.

In conclusione, il circuito integratore funziona correttamente in una banda di frequenza compresa tra f₁ e f₂ .

Per frequenze inferiori a quella del polo f_t = 1 / (2p R₁C), o per eventuali componenti continue, il circuito si comporta da amplificatore invertente con amplificazione - R₁/R.

La larghezza di banda utile, ai fini di un utilizzo del circuito come integratore, può essere così ricavata:

                                                              .                                   (3.22)

Da tale relazione, supponendo di potere fissare a priori la larghezza di banda B del segnale utilizzato in ingresso, possiamo scrivere la relazione che intercorre fra i valori di R e R₁, e quindi l’amplificazione in continua necessaria, in funzione di B e di C. Risolvendo la (3.22) rispetto R₁, si ha: