4.4. - Risposta in frequenza di un derivatore reale.
Possiamo scrivere la funzione di trasferimento per il circuito derivatore reale, considerando che nella
![]() è
è ![]() .
.
Sostituendo, si ha:
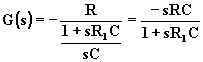 (4.6)
(4.6)
La funzione di trasferimento presenta uno zero nell’origine e un polo negativo S= - 1/R1C.
In regime sinusoidale, si ha s = jw . Sostituendo nella ( 4.6 ), si ha:
![]() (4.7)
(4.7)
Il cui modulo e fase sono:
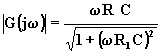
![]() .
.
In decibel si ha:
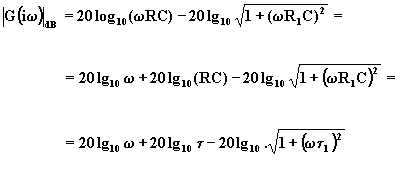 (4.8)
(4.8)
Al fine di tracciare l’andamento, si esaminano i seguenti tre casi:
a.- ![]() (4.9)
(4.9)
che nel diagramma di Bode di fig. 4.3 rappresenta una retta con pendenza positiva di 20dB/decade che interseca l’asse delle ordinate nel punto
![]()
è l’asse delle ascisse in w = 1 / t .
b.-
![]()
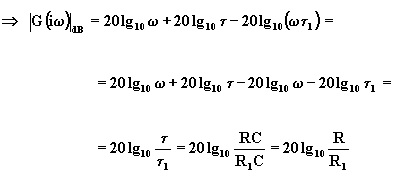
che nel diagramma di Bode rappresenta una retta parallela all’asse delle ascisse e interseca l’asse delle ordinate in 20lg10R/R1.
Le due rette si intersecano nel punto di ascissa w = 1 / t 1, polo dell’equazione (4.6) e ordinata 20lg10R/R1.
c.-
![]()
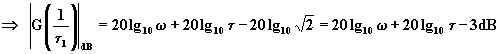 ,
,
ossia nell’intorno del polo la risposta si discosta dal diagramma asintotico di Bode per un massimo di –3dB per w = 1 / t 1.
L'approssimazione è ben verificata per w < 0 . 1 / t 1 e w > 1 0 / t 1.
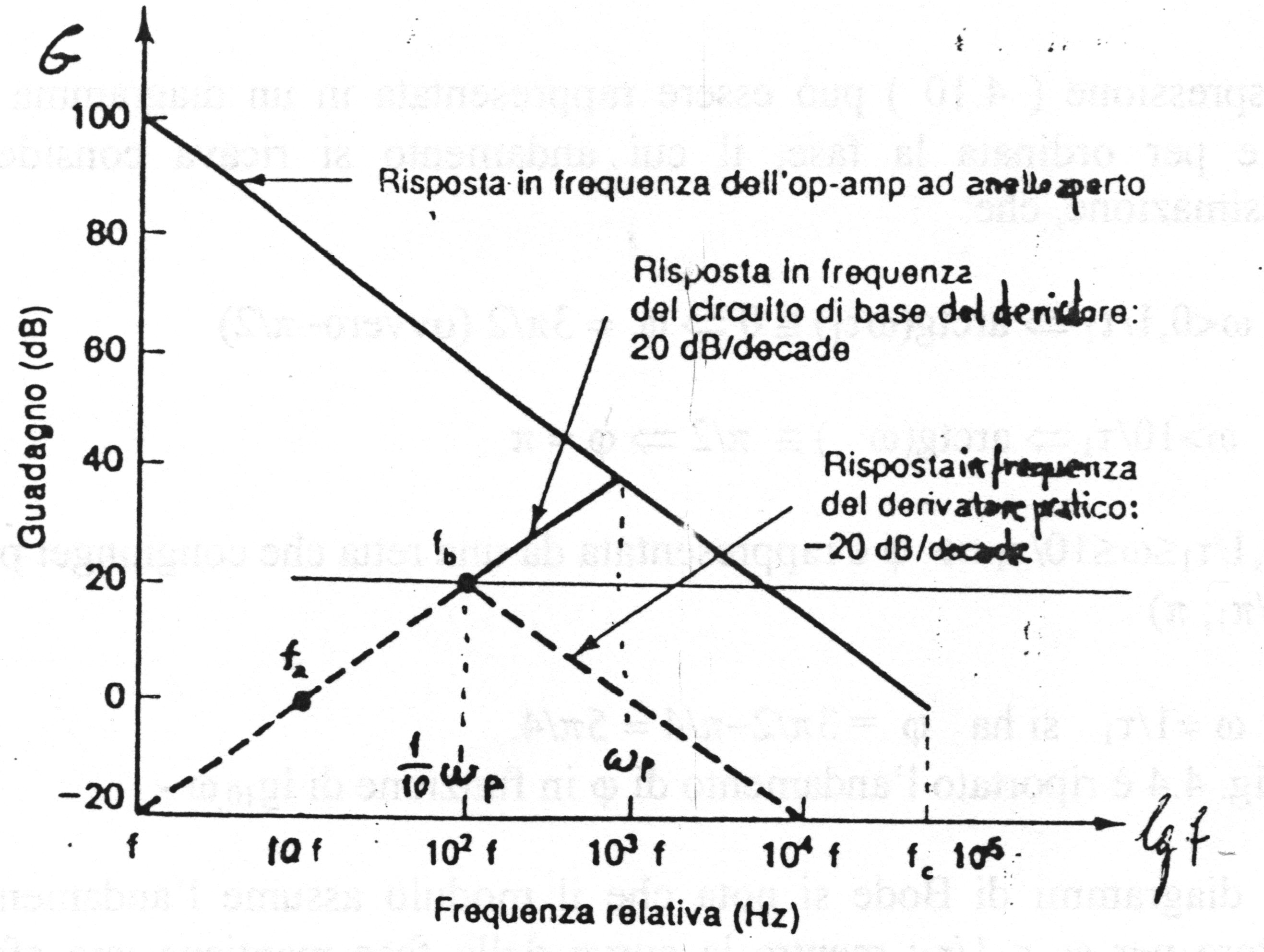
Fig. 4.3 Diagramma di Bode dell'ampiezza
La risposta in fase è:
![]() (4.10)
(4.10)
L’espressione ( 4.10 ) può essere rappresentata in un diagramma avente per ascissa lg10w e per ordinata la fase, il cui andamento si ricava considerando, con buona approssimazione, che:
a.- w < 0 ,1 /t 1 Þ arctg( w t 1) @ 0 Þ j = 3 p / 2 ( ovvero- p / 2 )
b.- w > 1 0 / t 1 Þ arctg(w t 1) @ p / 2 Þ j = p
c.- 0 , 1/ t 1 £ w £ 10/t 1 Þ j è rappresentata da una retta che congiunge i punti
( 0 , 1 / t 1 ; 3 p / 2 ) e ( 1 0 / p 1 ; p ) .
Per w = 1 / t 1 si ha : j = 3 p / 2 - p / 4 = 5 p / 4 .
In fig. 4.4 è riportato l’andamento di j in funzione di lg10 w .
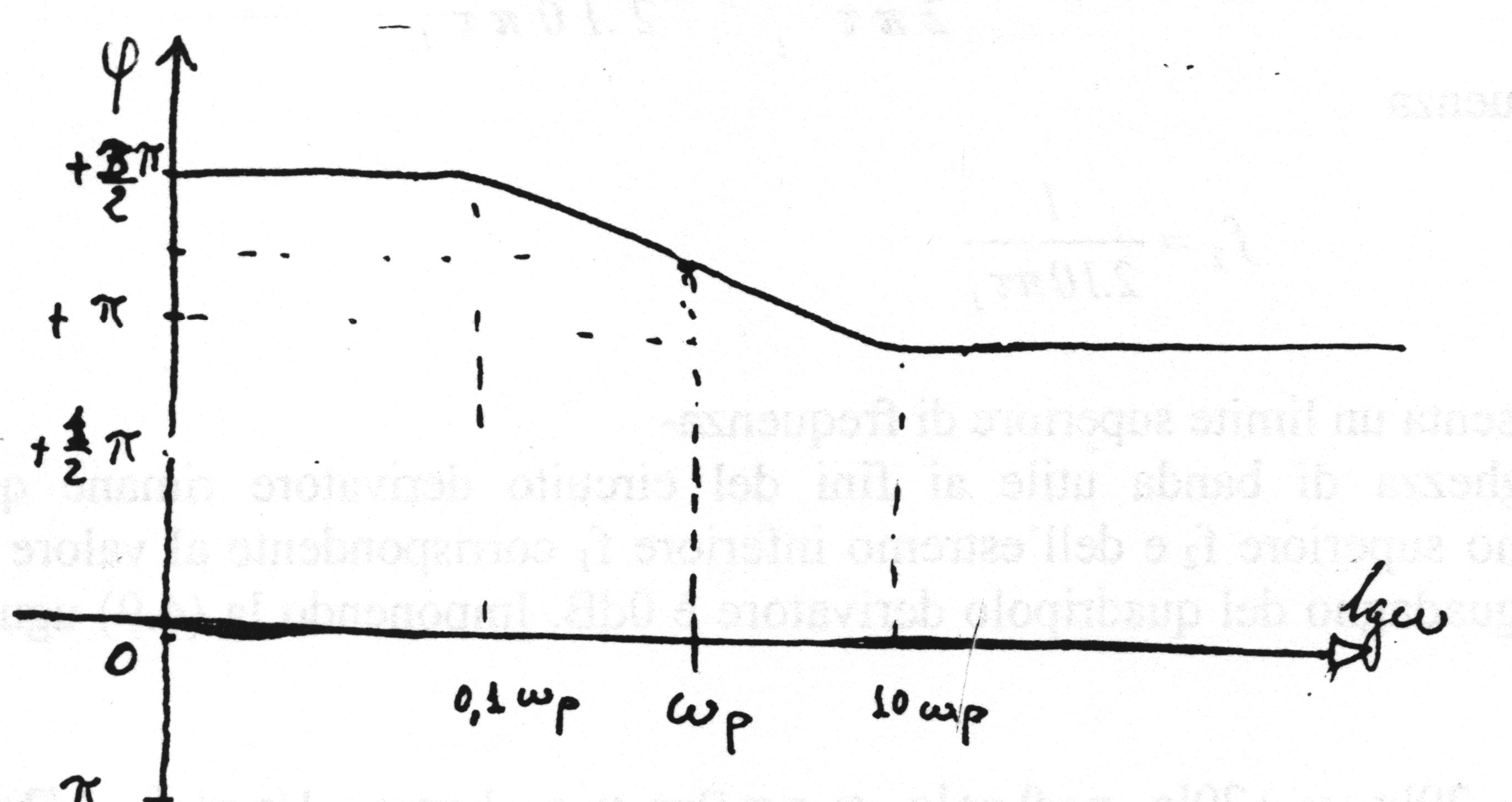
Fig. 4.4 Diagramma di Bode della fase
Dai diagrammi di Bode si nota che il modulo assume l’andamento di quello di un derivatore per w < 1/ t 1; mentre la curva della fase mantiene uno sfasamento di 90o in ritardo con buona approssimazione solo per w £ 0 , 1 / t 1. Conseguentemente, se f è la frequenza del segnale, il circuito si comporta da derivatore per
w £ 0 , 1 / t 1
ossia
![]() .
.
La frequenza
![]() (4.11)
(4.11)
Rappresenta un limite superiore di frequenza-
La larghezza di banda utile ai fini del circuito derivatore rimane quindi fissato dall’estremo superiore f2 e dall’estremo inferiore f1 corrispondente al valore di frequenza per cui il guadagno del quadripolo derivatore è 0dB. Imponendo la (4.9) uguale a zero, si ottiene:
![]() (4.12)
(4.12)
Pertanto, la larghezza di banda è: B = f2 - f1 ( 4.13 )
Sostituendo nella (4.13 ) le ( 4.11 ) e ( 4.12 ), si ha:
![]() (4.14)
(4.14)
Da quest’ultima relazione, una volta definita la larghezza di banda B del segnale utilizzato in ingresso, si può ricavare la relazione che intercorre tra i valori di R1 e R, e quindi l’amplificazione massima necessaria, in funzione di B e di C:
![]() (4.15)
(4.15)
Da questa espressione si ha che per B = 0, ossia frequenza unica di ingresso, si ha: R = 10R1.
Mentre, per un dato valore di B > 0, e un definito valore di C, si può osservare che il valore di R dovrà essere maggiore di 10R1, ciò vuol dire che occorre utilizzare un valore di amplificazione più elevato. La massima larghezza di banda, oltre ad essere limitata dalle caratteristiche intrinseche del circuito integrato, viene anche fissata dalla (4.15), quando il suo denominatore tende a zero, ossia:
![]()
Per tale valore di B, infatti, R tende all’infinito, cioè si ha un funzionamento ad anello aperto, rendendo irrealizzabile la derivazione.