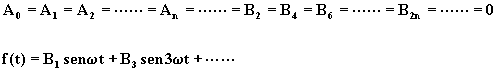A.4. - Sviluppo di serie di Fourier di segnali periodici
Una funzione periodica del tempo, di determinata frequenza f, può essere scomposta nella somma di un termine costante di infiniti termini sinusoidali e cosinusoidali di ampiezza opportuna e frequenza uguale e multipla di quella data.
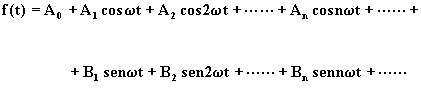
Dove A0 è un termine costante, il cui valore è quello del valore medio della funzione data:
mentre i coefficienti de seni e dei coseni si ottengono dalle formule:
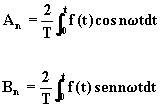con n=1, 2,…..
Si esaminano alcuni casi particolari.
Se la funzione è simmetrica rispetto all’asse delle ordinate, si definisce pari
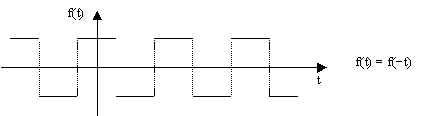
allora nello sviluppo di Fourier si annullano i termini sinusoidali, cioè sono nulli i coefficienti Bn, per cui lo sviluppo risulta formato dai soli termini cosinusoidali e dal termine costante:
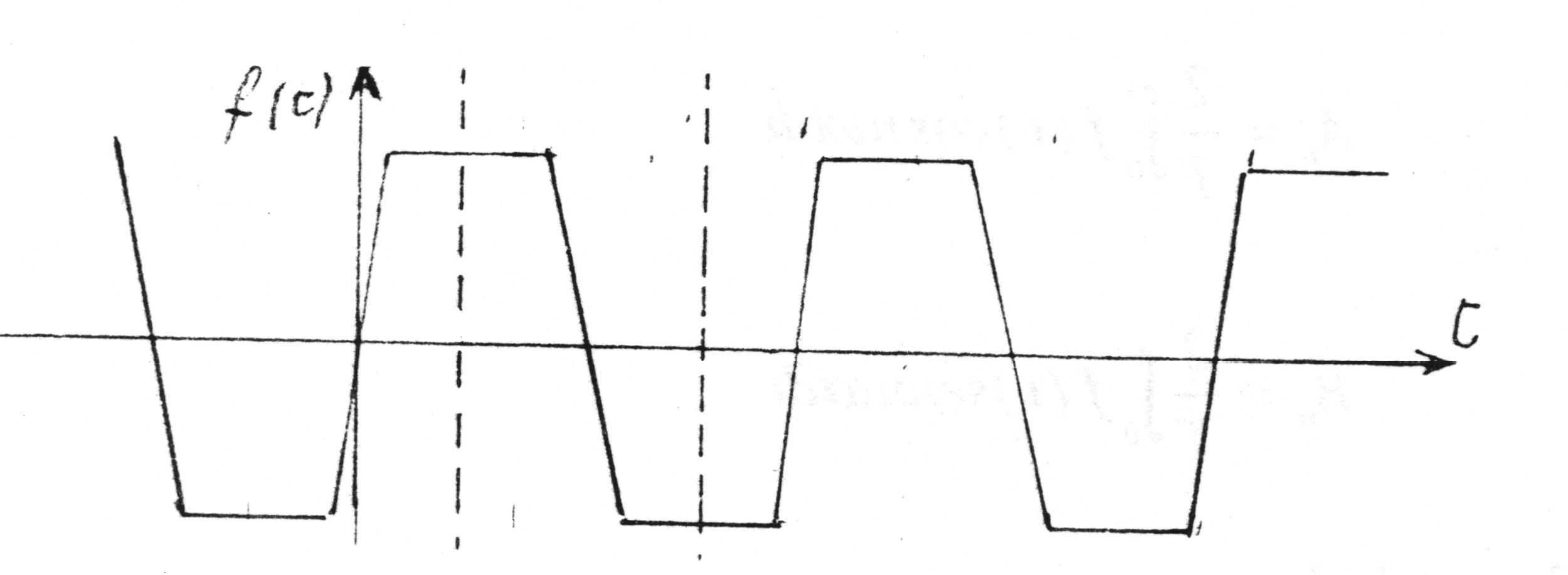
Se la funzione periodica è antisimmetrica rispetto all’asse delle ordinare (simmetrica rispetto all’origine) si dice dispari:
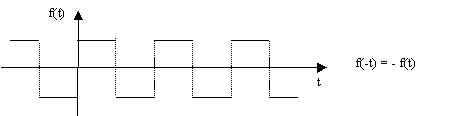
allora nello sviluppo di Fourier sono nulli i coefficienti A0 e An, per cui lo sviluppo è formato dai soli termini sinusoidali:
Se la funzione periodica è anche alternativa(a valore medio nullo) con semiperiodi non simmetrici rispetto
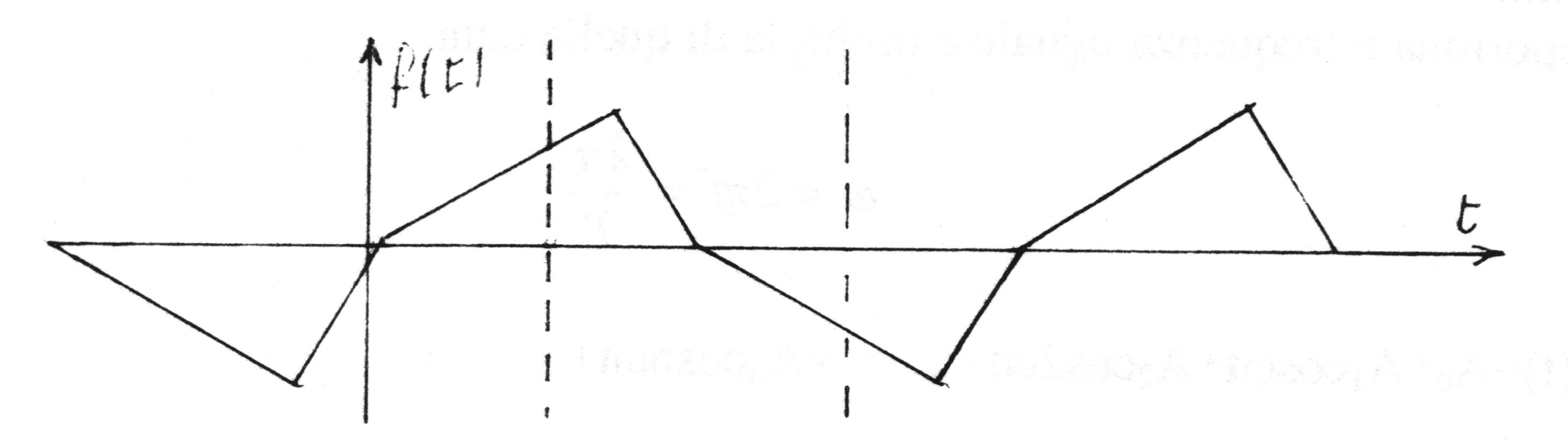
all’asse medio del semiperiodo, il suo sviluppo manca delle armoniche di ordine pari, cioè:
Se la funzione periodica è alternativa con semiperiodi simmetrici rispetto all’asse medio del semiperiodo, lo sviluppo manca delle armoniche di ordine pari e dei termini cosinusodali:
