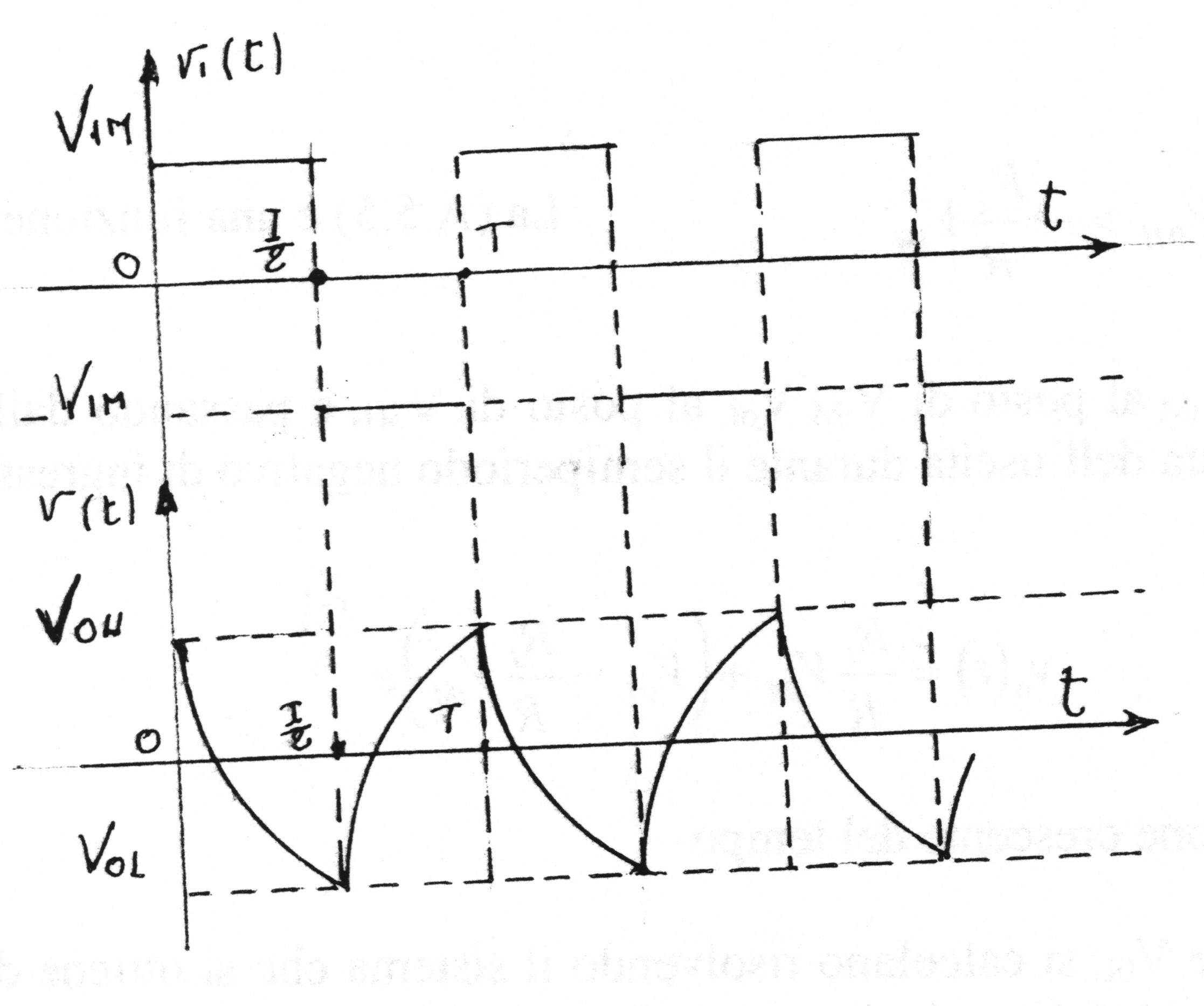
A.5.1. - Risposta all’onda quadra a valore medio nullo

Si risolve la (A.5.4) con vi(t) = ViM
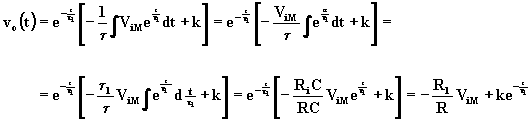
La costante k si ricava imponendo che al tempo t = 0 la tensione di uscita è vo(0) = VoH:
![]() .
.
Sostituendo si ha:
![]() (A.5.5)
(A.5.5)
La (A.5.5) è l’equazione di carica e di scarica di una capacità. Confrontando con l’equazione generale
![]() ,
,
Si ha: valore iniziale a t = 0 Þ vo(0) = VoH
valore finale a t = ¥ Þ vo( ¥ ) = - (R1/R)ViM.
Poiché ![]() , la (A.5.5) è
una funzione decrescente del tempo.
, la (A.5.5) è
una funzione decrescente del tempo.
Sostituendo –ViM al posto di ViM, VoL al posto di VoH, e passando dalla variabile t a (t - T/ 2 ), si ottiene la risposta dell’uscita durante il semiperiodo negativo di ingresso:
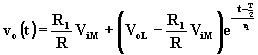 (A.5.6)
(A.5.6)
che è una funzione crescente del tempo.
I valori di VoH e VoL si calcolano risolvendo il sistema che si ottiene dalla (A.5.5) calcolata a t = T/2 e dalla (A.5.6) calcolata a t = T; a tali valori le (A.5.5) e (A.5.6) assumono rispettivamente i valori VoL e VoH:
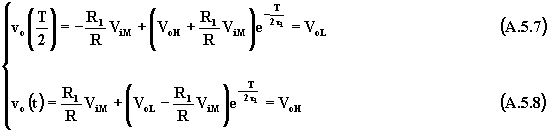
Sostituendo la (A.5.7) nella (A.5.8) al posto di VoL si calcola, VoH:
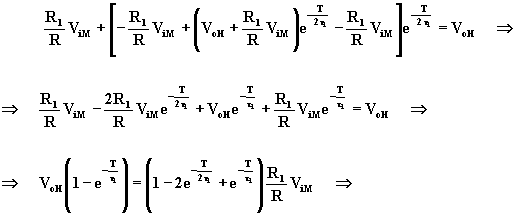
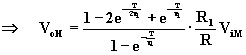 (A.5.9)
(A.5.9)
Sostituendo la (A.5.8) nella (A.5.7) al posto di VoH, si calcola Vol:
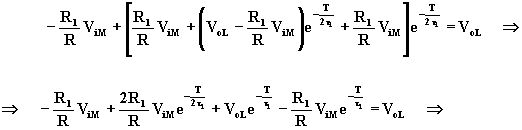
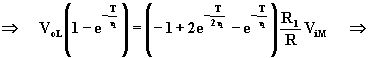
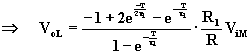 (A.5.10)
(A.5.10)
Confrontando la (A.5.9) e la (A.5.10), è immediato notare che:
VoH = - VoL,
ossia l’uscita oscilla attorno allo zero (che in questo caso è anche il valore medio del segnale di ingresso).
Perché l’uscita sia una rampa lineare, la scarica e la carica della capacità C deve avere una durata molto minore della costante di tempo t 1. In tale caso si è nel primissimo tratto della curva di carica e scarica che può essere approssimato mediante una retta, ossia sostituendo a
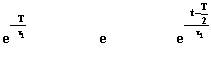
i loro sviluppi in serie di Mac Laurin arrestati alla prima potenza.
La durata della carica e scarica è definita dalla durata del semiperiodo del segnale di ingresso’ ossia:
![]() .
.
La serie di Mac Laurin dell'esponenziale ex è:
![]() .
.
Lo sviluppo di ![]() è:
è:
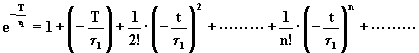 ,
,
e di ![]() è:
è:
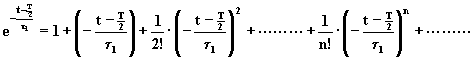 .
.
Sostituendo nella (A.5.7) e nella (A.5.8), e arrestando lo sviluppo alla prima potenza si ha:
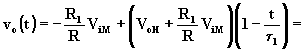
![]()
![]() rampa decrescente (A.5.11)
rampa decrescente (A.5.11)
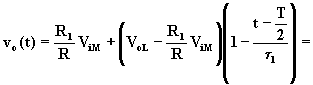
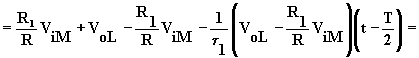
![]() rampa crescente
(A.5.12)
rampa crescente
(A.5.12)
I valori di VoH e VoL si calcolano risolvendo il sistema che si ottiene dalla (A.5.11) calcolata a t = T/2 e dalla (A.5.12) calcolata a t = T; a tali valori le (A.5.11) e (A.5.12) assumono rispettivamente i valori VoL e VoH:
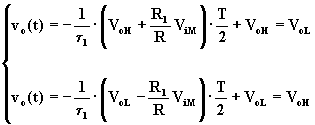
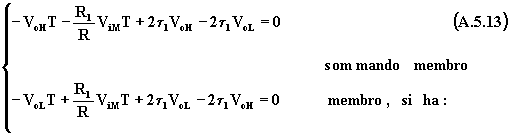
____________________________________
![]() .
.
Sostituendo nella (A.5.13) - VoH al posto di VoL, si ha:
![]()
![]()
Poiché T < < t 1 Þ 4 t 1- T @ 4 t 1, per cui
![]() (A.5.14)
(A.5.14)
Sostituendo la (A.5.14) nella (A.5.11), si ha:
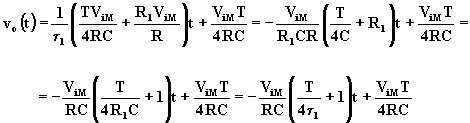
Poiché T < < t 1 Þ T < < 4 t 1 Þ T / 4 t 1 < < 1 Þ T / 4 t 1 è un termine trascurabile rispetto ad 1, per cui si ha l’equazione della rampa decrescente:
![]() (A.5.15)
(A.5.15)
Le (A.5.14) e (A.5.15) sono state ottenute già nel capitolo 5. Ad analogo risultato si perviene sostituendo la (A.5.14) cambiata di segno nella (A.5.12) per la rampa crescente.