1.6.2. - Risposta nello stato zero

L'integrale particolare dell'equazione completa dipende dalla forma d'onda del segnale applicato al circuito a partire dall'istante t = 0. Supponendo che esso sia costante di ampiezza V_i, si ha in uscita una tensione V_o anch'essa costante. La soluzione completa sarà:

Radici reali distinte

                                                                                         (1.6.26)

Supponendo che il circuito si trovi nello stato zero nell'istante iniziale t = 0, e che in tale istante , si ricavano K₁ e K₂.

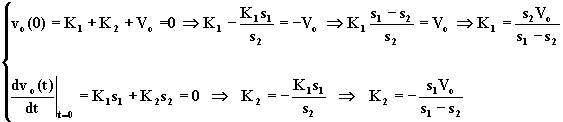
Sostituendo nell'equazione (1.6.26), si ottiene:

                                                                               (1.6.28)

Radici reali coincidenti

                                                                                         (1.6.29)

Imponendo che il circuito si trovi nello stato zero nell'istante iniziale t = 0, e che in tale istante , si ricavano K₁ e K₂.

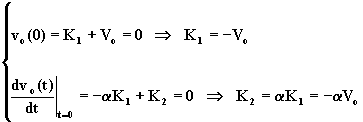                                                                       (1.6.30)

Sostituendo nell'equazione (1.6.29), si ottiene:

                                                                                        (1.6.31)

Radici complesse coniugate

Conviene esprimere la (1.6.28) in forma diversa, utilizzando lo stesso procedimento seguito per ricavare l'equazione (1.6.24). segue:

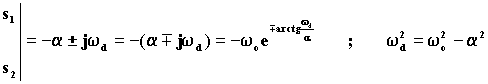
                                                                                         (1.6.31)

Imponendo che il circuito si trovi nello stato zero nell'istante iniziale t = 0, e che in tale istante , si ricavano K₁ e K₂.

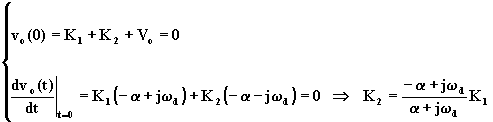
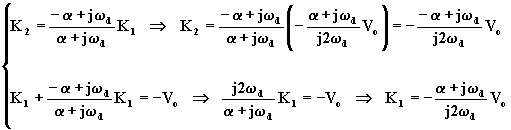
Sostituendo nell'equazione (1.6.31), si ottiene:

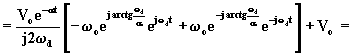
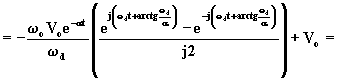
                                                         (1.6.32)

In figura è riportato l'andamento della risposta ad un gradino di tensione per un circuito sovrasmorzato e per uno sottosmorzato.

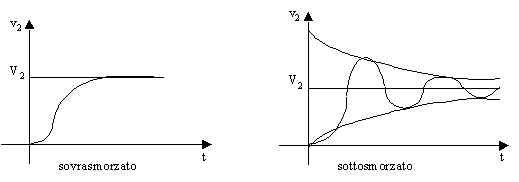
In un circuito sovrasmorzato la risposta tende al suo valore finale senza mai superarlo; in uno sottosmorzato la risposta oscilla smorzandosi attorno al suo valore finale.