6.1. – Approssimazione di butterworth
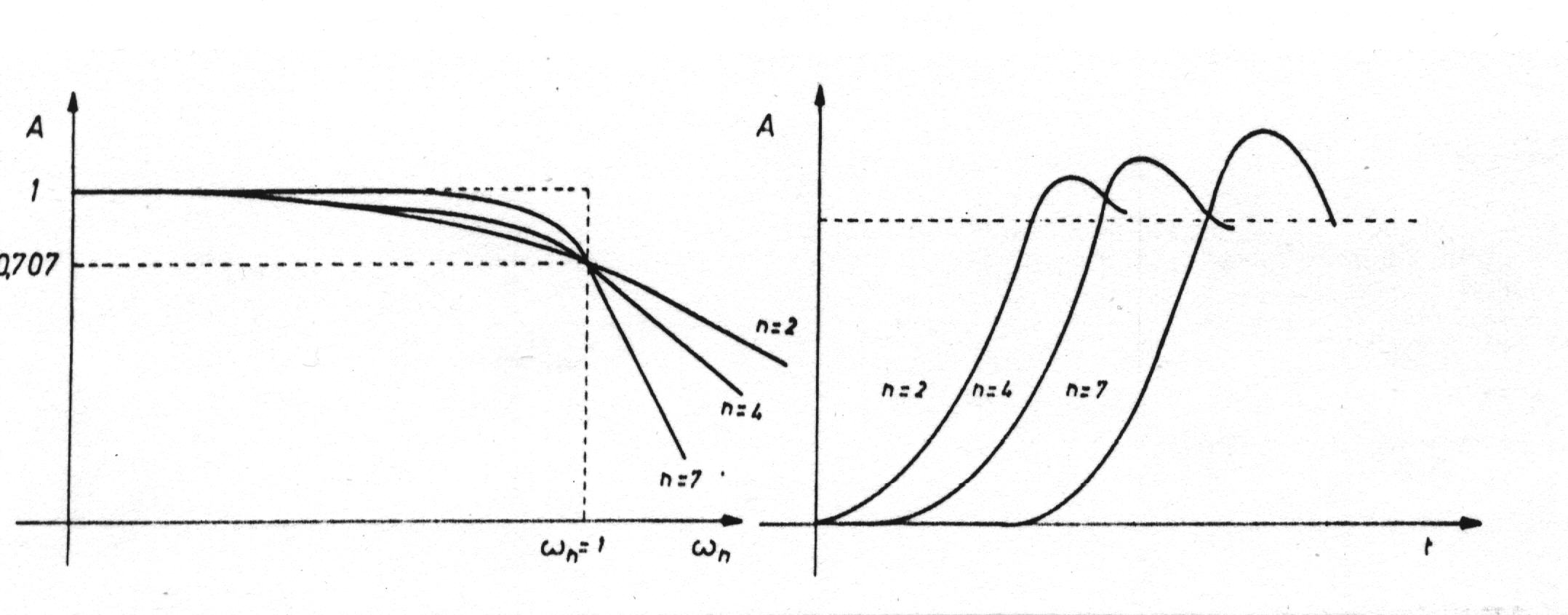
I filtri di Butterworth sono anche chiamati filtri a banda massimamente piatta, poiché la risposta in ampiezza è estremamente piatta nell'intorno di w = 0.
In figura sono mostrate le risposte in frequenza e la risposta temporale ad un gradino di un filtro passa-basso di Butterworth per vari valori del parametro n, che rappresenta l'ordine della f.d.t. (detto anche ordine del filtro).
È da notare che la risposta in frequenza è riportata in funzione di wn (pulsazione normalizzata), dove
,
fo è detta frequenza di taglio del filtro.
Come si è già detto, all'aumentare di n la risposta in frequenza del filtro si avvicina a quella ideale.
La f.d.t. di un filtro di Butterworth passa basso è così definita:
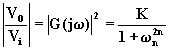
dove K è definito fattore di amplificazione e n è l'ordine del filtro.
Dalla precedente relazione si può vedere che per 
(cioè per w = w o). Questo indica che la frequenza alla quale il
guadagno si riduce di 3dB è indipendente da n.
Nella tabella sono riportati i polinomi in s di Butterworth (corrispondenti ai denominatori delle f.d.t.) per valori di n compresi tra 1 e 5.
n |
Polinomi di Butterworth |
1 |
S+1 |
2 |
S2+sÖ 2+1 |
3 |
(s2+s+1)(s+1) |
4 |
(s2+0,7653s+1) (s2+1,8478s+1) |
5 |
(s+1) (s2+0,6180s+1) (s2+1,6180s+1) |
La risposta al gradino presenta un overshoot e un settling time contenuti; i loro valori crescono comunque con l'ordine del filtro.
Il progetto e la messa a punto dei filtri alla Butterworth è relativamente agevole ed essi sono discretamente diffusi in campo audio dove la scarsa linearità della curva di fase in banda passante e, quindi, la distorsione di fase non costituiscono un problema rilevante.
