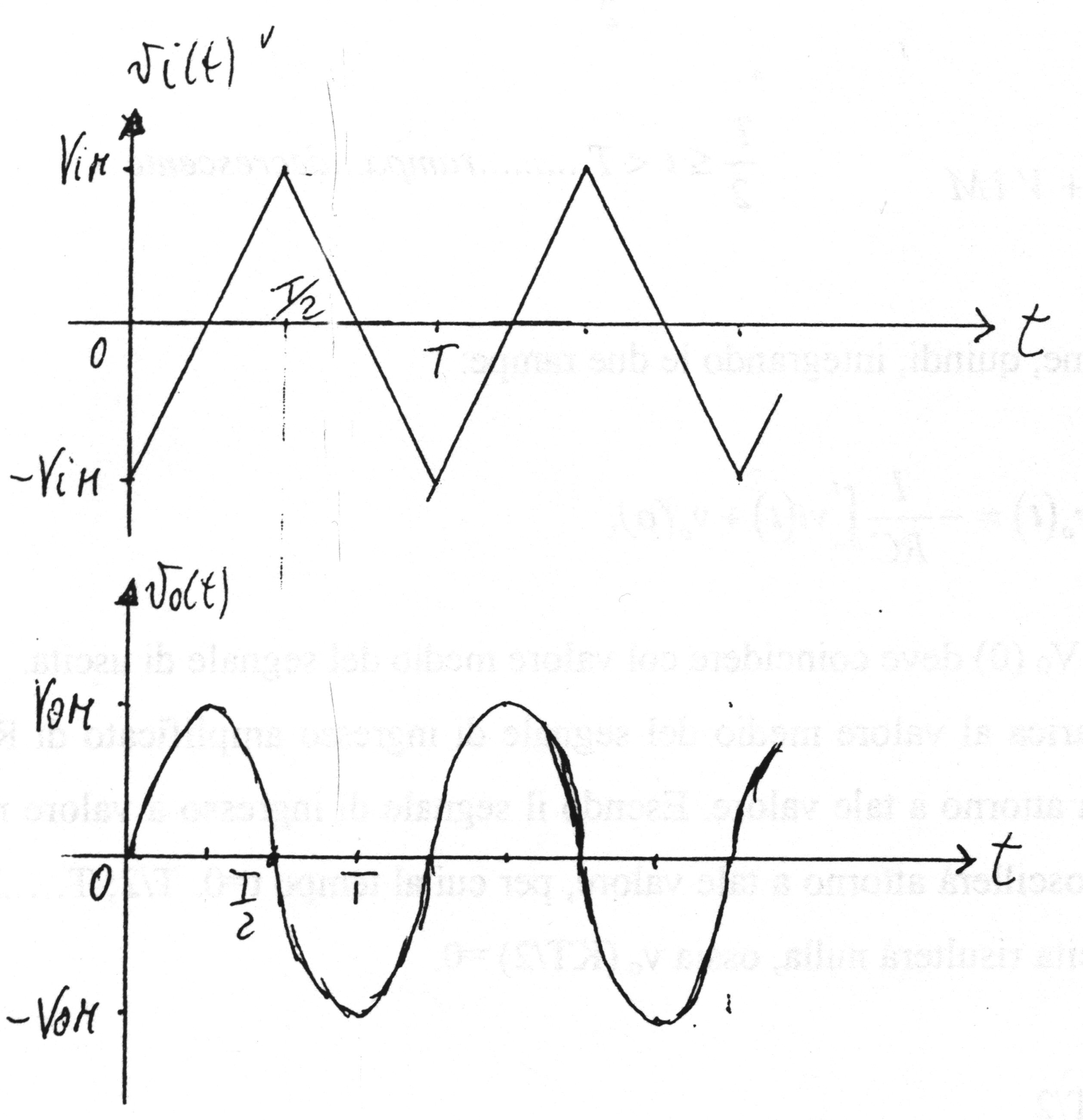
5.5.3. - Onda triangolare a valore medio nullo

Si ricava l’equazione del segnale di ingresso, calcolando le equazioni delle rampe crescente e decrescente come rette passanti per un punto e di dato coefficiente angolare:

a.- Rampa crescente 0 £ t < T/2:

                                                                    (5.14)

b.- Rampa decrescente T/2 £ t < T

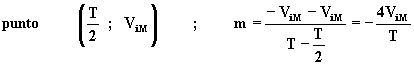
                                                                     (5.15)

Associando le (5.14) e (5.15), si ha il segnale di ingresso:

Il segnale di uscita si ottiene, quindi, integrando le due rampe:

,

dove v_o(0) = 0, in quanto v_o(0) deve coincidere col valore medio del segnale di uscita.

Poiché la capacità C si carica al valore medio del segnale di ingresso amplificato di R₁/R e invertito, l’uscita oscillerà attorno a tale valore. Essendo il segnale di ingresso a valore medio nullo, il segnale di uscita oscillerà attorno a tale valore, per cui al tempo t = 0, T/2, T,…,KT/2, con K = 0, 1, 2_,…….., l’uscita risulterà nulla, ossia v_o(KT/2) = 0.

a.- Rampa crescente, 0 £ t < T/2

                                                                                                                      (5.16)

La (5.16) è l’equazione di una parabola con la concavità rivolta verso il basso, che interseca l’asse dei tempi nei punti:

(0 , 0)           e           (T/2 , 0),

e raggiunge il valore massimo per t = T/4

                                                                                  (5.17)

b.- Rampa decrescente, T/2 £ t < T

                                                                                                           (5.18)

La (5.18) è l’equazione di una parabola con la concavità rivolta verso l’alto, che interseca l’asse dei tempi nei punti

(T/2 , 0)           e           (T , 0),

e raggiunge il valore minimo per t = 3(T/4)