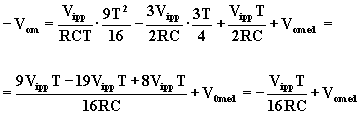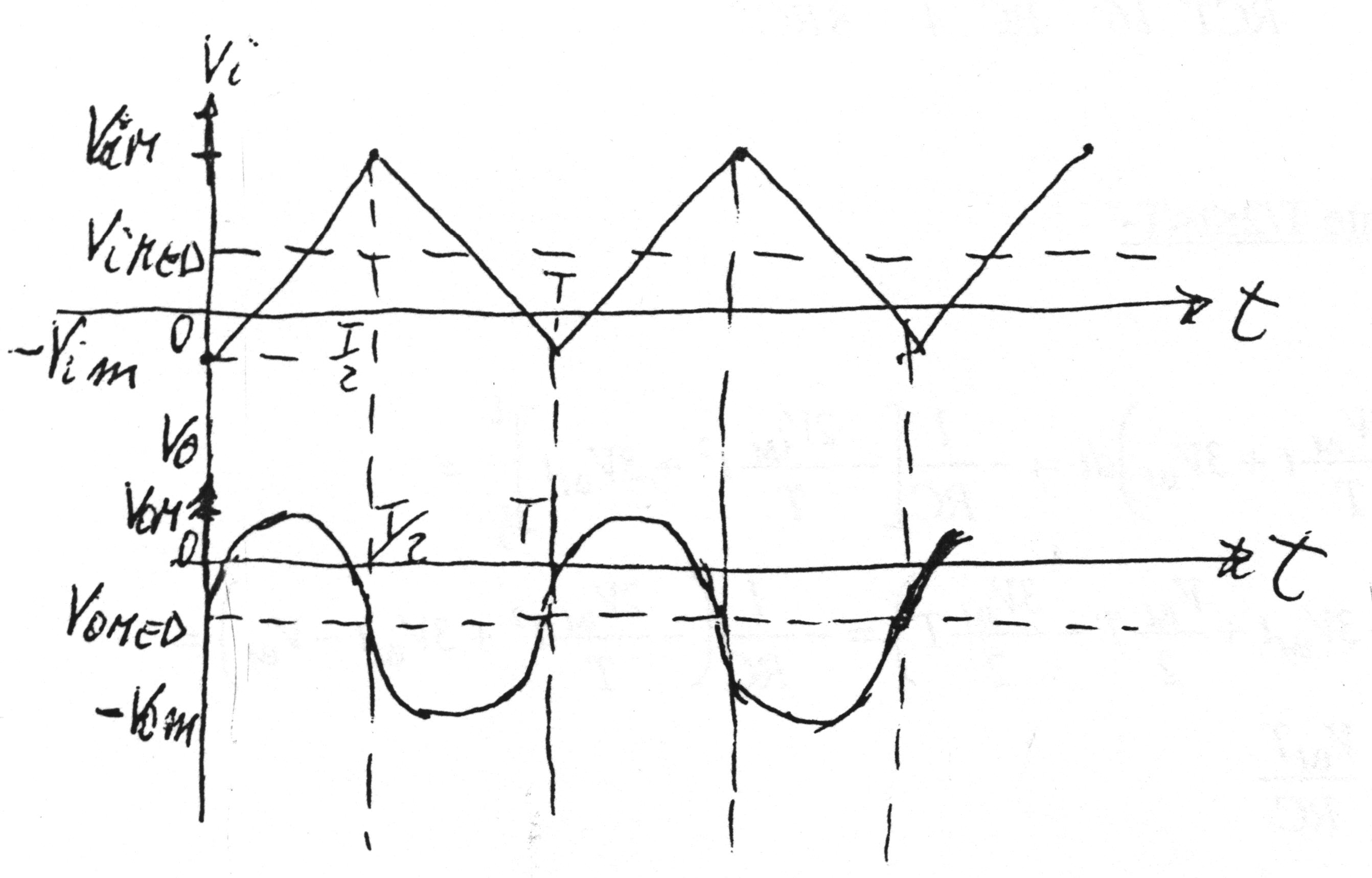
5.5.4. - Onda triangolare a valore medio non nullo
Se il segnale di ingresso è a valore medio non nullo, Vimed, il condensatore si caricherà alla tensione costante Vomed e l’uscita oscillerà attorno a tale valore.
Si pone
Il segnale di ingresso Vi equivale alla somma (o sovrapposizione) di un segnale triangolare a valore medio nullo e ampiezza Vipp/2 e di un segnale continuo pari al valore medio del segnale di ingresso, Vi med. In tale ipotesi, l’equazione del segnale di ingresso è:
a.- rampa crescente, 0 £ t < T/2
Retta per il punto (-Vim , 0) di coefficiente angolare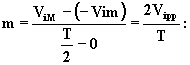 
(5.19)
b.- rampa decrescente, T/2 £ t < T
retta per il punto (ViM , T/2) di coefficiente angolare
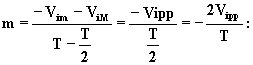
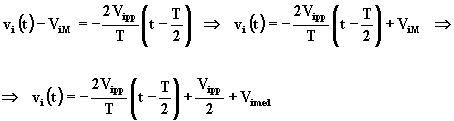(5.20)
Il segnale di ingresso è quindi esprimibile come sovrapposizione del segnale alternato
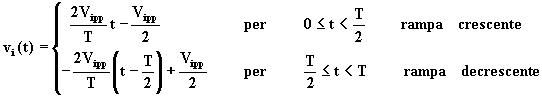
e del segnale continuo Vimed.
Il segnale di uscita si otterrà, quindi, dalla sovrapposizione degli effetti del segnale continuo e di quello alternato.
a.- Effetto sull’uscita del segnale continuo Vimed di ingresso
Il circuito, rispetto al segnale continuo, ossia a frequenza nulla, si comporta da amplificatore invertente con guadagno R1/R= 10. In uscita si avrà:
(5.21)
b.- Effetto sull’uscita del segnale triangolare di ingresso a valore medio nullo
rampa crescente, 0 £ t < T/2
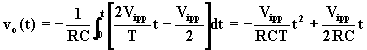(5.22)
rampa decrescente, T/2 £ t < T
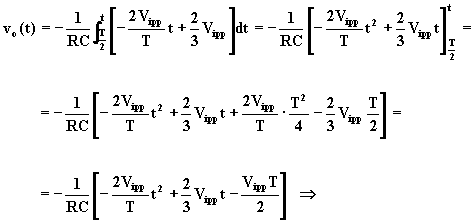
(5.23)
Il segnale di uscita si ottiene dalla sovrapposizione del segnale continuo (5.21) e del segnale alternato dato dalle (5.22) e (5.23).
a.- uscita relativa alla rampa crescente di ingresso, 0 £ t < T/2
(5.24)
La (5.24) è l’equazione di una parabola con la concavità rivolta verso il basso, che inizia e finisce nei punti
(0 ; Vomed) e (T/2 ; Vomed)
e raggiunge il valore massimo per t = T/4:
.
b.- uscita relativa alla rampa decrescente di ingresso, T/2 £ t < T
(5.25)
La (5.25) è l’equazione di una parabola con la concavità rivolta verso l’alto che inizia e finisce nei punti
(T/2 ; Vomed) e (T ; Vomed)
e raggiunge il valore minimo per t = 3T/4:
